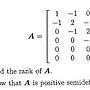討論串(共4篇) - [線代] 半正定矩陣一題 - 看板Math

看板 [ Math ]

討論串[線代] 半正定矩陣一題

共 4 篇文章

排序：最新先 | 最舊先 | 留言數 | 推文總分

內容預覽：開啟 | 關閉 | 只限未讀

首頁

尾頁

Re: [線代] 半正定矩陣一題

推噓0(0推 )留言0則，0人參與作者XII (Mathkid)時間7年前 (2019/01/19 11:06)資訊

內容預覽:

這個矩陣 A 是 P_6 的 Laplace matrix, 其中 P_6 為 6 個點的 path. 一般而言,. 圖 G=(V,E) 的 Laplace matrix L(G) (|V|×|V| 的方陣) 的定義是:. L(G)_{u,v} := { deg(u) if u=v in V. {

(還有293個字)

Re: [線代] 半正定矩陣一題

推噓0(0推 )留言0則，0人參與作者Vulpix (Sebastian)時間7年前 (2019/01/18 10:16)資訊

內容預覽:

可以用 Cholesky decomposition 爆他。. A 差不多是二階差分矩陣，. 所以 A 的 Cholesky decomposition 差不多會是一階差分^2。. 不過沒感覺到這個現象，也一樣可以算分解。. B_ij = 1, i=j<n. -1, j=i+1. 0, otherw

(還有407個字)

Re: [線代] 半正定矩陣一題

推噓2(2推 )留言2則，0人參與作者Eliphalet (高等遊民)時間7年前 (2019/01/18 07:11)資訊

內容預覽:

不要硬幹啦.... 這個可以用 Gershgorin disk theorem. 1. 這個矩陣的 eigenvalue 都是實數. 2. 套 Gershgorin disk theorem 加上 1 可以得知特徵值大於等於0. 3. A半正定. --. ※ 發信站: 批踢踢實業坊(ptt.cc),

[線代] 半正定矩陣一題

推噓4(4推 )留言7則，0人參與作者cevian (cevian)時間7年前 (2019/01/18 01:44)資訊

內容預覽:

https://i.imgur.com/keb74uF.jpg. 想請教的是第二小題. 證明A是半正定矩陣. 目前的想法是. 因為題目是實對稱矩陣. 所以找出它全部的特徵值. 特徵值有0跟其他正數. 就是半正定. 但…剛才實際一做. 發現整個乘開蠻複雜的. 而且我找出來的特徵值全部都是正的……（不知

(還有81個字)

首頁

尾頁