討論串(共7篇) - [幾何] 一題幾何證明請教~ - 看板Math

看板 [ Math ]

討論串[幾何] 一題幾何證明請教~

共 7 篇文章

排序：最新先 | 最舊先 | 留言數 | 推文總分

內容預覽：開啟 | 關閉 | 只限未讀

首頁

尾頁

Re: [幾何] 一題幾何證明請教~

推噓2(2推 )留言2則，0人參與作者Honor1984 (奈何上天造化弄人？)時間7年前 (2018/06/24 02:51)資訊

內容預覽:

命題正確. BD中點G，EC交BD於H. 因為∠GED + ∠EDC = 180 => EG // DC. => EGCD為平行四邊形 => ED = GC. => △GCB = △DEC. 又∠DCE = ∠GBC = ∠ACF. => ∠CED = ∠ECG = ∠ECA + ∠ACG. = ∠

[幾何] 一題幾何證明請教~

推噓1(1推 )留言2則，0人參與作者nokol (騷人墨客)時間7年前 (2018/06/23 18:15)資訊

內容預覽:

http://i.imgur.com/fsB32v7.jpg. 想請教站上大師指點. 感謝您，先謝謝您. 謝謝. -----. Sent from JPTT on my Samsung SM-G955F.. --. ※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 180.204.3.67. ※

Re: [幾何] 一題幾何證明請教~

推噓0(0推 )留言0則，0人參與作者wayne2011 (今年十三號星期五)時間8年前 (2018/01/03 16:23)資訊

內容預覽:

參考. 黃家禮. 所編著的"幾明". 當中的例題. 可知b^2=c(c+a). 於是乎. DA=c/2,EF=(a/2)-ccosB=(a/2)-[(c^2+a^2-b^2)/2a]=(a/2)-[(a-c)/2]=c/2,即證DA=EF.. --. ※ 發信站: 批踢踢實業坊(ptt.cc), 來

Re: [幾何] 一題幾何證明請教~

推噓2(2推 )留言2則，0人參與作者Tiderus (修煉人生)時間8年前 (2018/01/02 16:58)資訊

內容預覽:

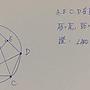
其實原本的圖上畫的線就可以證了。. AC平行DE --> ∠DEB = ∠C. ABF為直角Δ--> BD = DF = AD --> ∠B = ∠DFB= 2∠DEB. --> ∠DEF = ∠FDE --> FD = FE = DB = AD. --. ※ 發信站: 批踢踢實業坊(ptt.cc)

(還有52個字)

Re: [幾何] 一題幾何證明請教~

推噓0(0推 )留言0則，0人參與作者LPH66 (J∪$т М㎝iκä)時間8年前 (2018/01/02 03:50)資訊

內容預覽:

在 CF 上取 B' 使 BF = FB', 連 AB'. 易證 △ABF 全等於 △AB'F, 故 ∠AB'F = 2∠C. 再由外角關係推得 ∠B'AC = ∠C, 即 B'C = AB' = AB. 所以 BC = BF + FB' + B'C = 2BF + AB = 2BF + 2AD.

(還有595個字)

首頁

尾頁