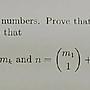看板
[ Math ]
討論串[離散] 一題離散
共 6 篇文章
內容預覽:
※ 引述《redcarp0702 (紅鯉魚)》之銘言. eminem2003 想法正確. 以下使用同樣的概念,寫簡潔一點. (Lem) 若 n, k 是正整數,0 <= m1 < m2 < ... < mk. 且已知 n = C(m1,1) + ... + C(mk,k). 則 mk 只有一個可能值
(還有640個字)
內容預覽:
寫了一個略嫌(?)粗糙的證明,待高手檢驗. 以下C(a,b)表示Ca取b. 題目是說任意給兩正整數n,k. 若存在由小到大的k個正整數,上面是寫m1~mk. 依序放到 C( ,1)+C( ,2)+C( ,3)+....C( ,k)的那些空白處. 也就是 C(m1,1)+C(m2,2)+C(m3,3)
(還有1603個字)
內容預覽:
http://i.imgur.com/pl9Hz6j.jpg. 目前學校剛教完計數原理,看完題目覺得跟二項式係數有關,但想了一個小時完全沒頭緒,m_k除了均為持續遞增的自然數外,就完全沒規律了,求解謝謝!!. -----. Sent from JPTT on my Sony E6853.. --.
(還有38個字)
內容預覽:
題目要的是一個 combinatorial proof.... (以下的 Σ 都是 k 從 1 到 n; 敘述中有關 k 的都是要從 1 到 n 全部算進去). Σk^2 C(n,k) 表示 n 個東西中取 k 個後在這 k 個當中可重覆地選兩個. 這樣的選法數如果先考慮選兩個的話有 n^2 種 (
(還有344個字)
內容預覽:
(1+x)^n = Σ[k;0,n] x^k C(n,k). differentiate it once. n(1+x)^{n-1} = Σ[k;1,n] k x^{k-1} C(n,k). 2n*2^{n-2} = Σ[k;1,n] k C(n,k). differentiate it twice
(還有38個字)