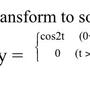Re: [其他] 求問一題Laplace transform

看板Math作者deathcustom (Full House)時間2年前 (2024/01/11 10:06)推噓2(2推 0噓 1→)

留言3則, 2人參與討論串2/2 (看更多)

※ 引述《chchunieh (ccwu)》之銘言： : 做到後面有點不知道怎麼做了，所以上來發文請教各位大大，非常感謝！ : https://i.imgur.com/dtKfZHl.jpg

: ---- : Sent from BePTT on my iPhone 11 左側L轉換: s^2Y+sY+Y 右側L轉換: 1. 先寫正規化的 cos(2t)u(t)-cos(2t)u(t-pi) 2. 將這個部分進行L轉換: 因為cos(2t) = cos(2(t-pi)) 所以可以寫為 s/(s^2+4)(1-exp(-pi*s)) 所以得到 Y = [1-exp(-pi*s)]*s/[(s^2+4)(s^2+s+1)] 後面就是你的事了XD -- ※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 211.23.191.211 (臺灣) ※ 文章網址: https://www.ptt.cc/bbs/Math/M.1704938777.A.B7C.html

→

musicbox810

01/11 10:17, 2年前 , 1^F

01/11 10:17, 1^F

推

chchunieh

01/11 10:26, 2年前 , 2^F

01/11 10:26, 2^F

s/[(s^2+4)(s^2+s+1)] 可以分解成 (As+B)/(s^2+4) + (Cs+D)/(s^2+s+1) As^3+As^2+As+Bs^2+Bs+B+Cs^3+4Cs+Ds^2+4D = s s^3: A+C = 0 s^2: A+B+D = 0 s^1: A+B+4C = 1 s^0: B+4D = 0 [1 0 1 0] [0] [1 1 0 1] [0] [1 1 4 0] x = [1] [0 1 0 4] [0] 解方程 B = -4D A = -C -C-3D = 0 C = -3D A:B:C:D = 3:-4:-3:1 B+3C = -4D-9D = 1 D = -1/13 C = 3/13 B = 4/13 A = -3/13 # 剩下真的是你的事了 ※ 編輯: deathcustom (211.23.191.211 臺灣), 01/11/2024 11:25:14

推

chchunieh

01/11 12:17, 2年前 , 3^F

01/11 12:17, 3^F

‣ 返回看板[ Math ] 數學

‣ 更多 deathcustom 的文章

文章代碼(AID): #1bdqqPjy (Math)