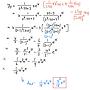Re: [其他] 逆運算求特解
※ 引述《Yic0197 (科科科55)》之銘言:
: 用逆運算子和答案少一項?
: 其他方法和解答一樣
: 想知道是因為在用逆運算子的時候不能分子分母對消?還是其他原因 謝謝
: https://i.imgur.com/Xwbm1s9.jpg

那條式子是這樣來的:
L(D)(xf) = xL(D)f + L'(D)f
然後把 f 用 L(D)\V 換掉,變成
L(D)(x[L(D)\V]) = xV + L'(D)[L(D)\V]
最後再整條式子都用 L(D) 左除
x[L(D)\V] = L(D)\(xV) + L(D)\L'(D)[L(D)\V]
移項完才得到
L(D)\(xV) = x[L(D)\V] - L(D)\L'(D)[L(D)\V]
一般情況下,因為 分母的 L(D) 與分子的 L'(D) 是可交換的,
所以我們並不在意順序,將最後一項寫作 L(D)^2\L'(D)V。
但這個寫法現在顯然有問題,因為此刻 L'(D)V = 0。
那我們大概也不能隨便亂約分了?這個問題晚點說明。
逆運算子法在某程度上是有點亂來的計算方式,所以有些規則會更嚴格。
例如運算的順序。
L(D)\L'(D)[L(D)\e^x]
= L(D)\L'(D)(x^2*e^x)/6
= L(D)\[(2x+1)e^x]
= 2L(D)\(xe^x) + (x^2*e^x)/2
= 2L(D)\(xV) + (x^2*e^x)/2
代回 L(D)\(xV) = x[L(D)\V] - L(D)\L'(D)[L(D)\V]
得到 L(D)\(xV) = (x^3*e^x)/6 - ( 2L(D)\(xV) + (x^2*e^x)/6 )
所以 (D^3-3D+2)\(xe^x) = (x^3*e^x)/18 - (x^2*e^x)/18
一般來說,這時候大概會抗議:
「可是V先積分再微分會變回V,這是微積分基本定理誒!為什麼不能約分啊?」
所以可以約分,但可以約分不代表可以交換。
被約掉的 D-1 在 L(D)\L'(D)[L(D)\e^x] 裡面藍色的那邊。
所以在 D+1 運算上去之前,一定要先運算一次 (D-1)^-1。
這已經是最低限度的妥協了。
在函數空間的其他地方,交換性通常都沒有問題,
但一扯到 多項式*e^x,那 (D-1)^-1 的順序就不能亂放了。
為了發新文章才發現即使有小心順序也還是不行。
最大的問題在於操作三次同一個逆運算,這已經超過原本容許範圍了。
多的那一次會造成一項係數待定項。
(如果多兩次就會有兩項,以此類推。)
另外,這題除了部份分式的做法,也比較適合這樣做:
(D-1)^2\[(D+2)\xe^x]
黃色部份可以直接用你喜歡的這條公式。
後面的計算也只是逆運算子的基本公式。
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 1.160.28.170 (臺灣)
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1628246497.A.B43.html
→
08/10 13:02, , 1F
08/10 13:02, 1F
→
08/10 13:03, , 2F
08/10 13:03, 2F
→
08/10 13:08, , 3F
08/10 13:08, 3F
→
08/10 13:08, , 4F
08/10 13:08, 4F
→
08/10 14:46, , 5F
08/10 14:46, 5F
→
08/10 14:47, , 6F
08/10 14:47, 6F
→
08/10 14:50, , 7F
08/10 14:50, 7F
→
08/10 14:51, , 8F
08/10 14:51, 8F
→
08/10 14:55, , 9F
08/10 14:55, 9F
→
08/11 14:42, , 10F
08/11 14:42, 10F
※ 編輯: Vulpix (163.13.112.58 臺灣), 08/18/2021 20:30:05
討論串 (同標題文章)