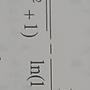Re: [微積] 問一題極限問題

: 試過了很多方法還是解不出來...
: 先謝謝各位。
:
很久沒解了 不知道有沒有更好的作法
y = ln(x+sqrt(x^2+1))
--> x = (1/2)(e^y - e^(-y)) = sinh(y)
1 1
lim [ ----------------- - --- ]
x->0 ln(x+sqrt(x^2+1)) x
1 1
= lim [ --- - ------- ]
y->0 y sinh(y)
sinh(y) - y
= lim [ ----------- ]
y->0 y sinh(y)
L cosh(y) - 1
= lim [ ----------------- ]
y->0 sinh(y)+ycosh(y)
L sinh(y)
= lim [ ----------------- ] = 0
y->0 2cosh(y)+ysinh(y)
1 1
lim [ --- - ------- ]
x->0 x ln(x+1)
ln(x+1) - x
= lim [ ----------- ]
x->0 x ln(x+1)
L 1/(x+1) - 1
= lim [ ---------------- ]
x->0 ln(x+1)+x/(x+1)
- x
= lim [ ---------------- ]
x->0 (x+1)ln(x+1) + x
L - 1 -1
= lim [ ----------- ] = ----
x->0 ln(x+1) + 2 2
因此答案是 -1/2 ow o
會想到 1/x 是因為本來就知道 lim_{x->0} ln(x+1)/x = 1
然後 sinh(x) 和 ln(x+1) 放一起實在太難算
--
嗯嗯ow o
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 117.19.67.76
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1546235034.A.F4B.html
推
12/31 15:31,
7年前
, 1F
12/31 15:31, 1F
→
12/31 15:31,
7年前
, 2F
12/31 15:31, 2F
→
12/31 15:31,
7年前
, 3F
12/31 15:31, 3F

→
12/31 15:32,
7年前
, 4F
12/31 15:32, 4F
→
12/31 15:46,
7年前
, 5F
12/31 15:46, 5F
推
12/31 16:50,
7年前
, 6F
12/31 16:50, 6F
→
12/31 16:51,
7年前
, 7F
12/31 16:51, 7F
→
12/31 16:51,
7年前
, 8F
12/31 16:51, 8F
討論串 (同標題文章)