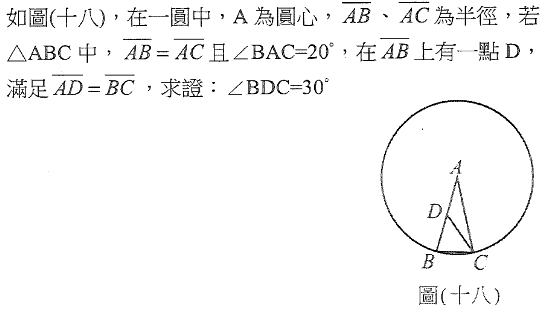
Re: [中學] 國中圓一題請教

: 請問應該如何下手?
: 先謝謝各位老師
假設
角CDB=alpha,(c-a)/sin[(5pi/9)-alpha)]=a/sin(alpha)
[sin(4pi/9)/sin(pi/9)]-1=sin[(4pi/9)+alpha]/sin(alpha)
sin[(4pi/9)+alpha]=sin(alpha)[4cos(pi/9)cos(2pi/9)-1]
sin(4pi/9)cos(alpha)=sin(alpha)[4cos(pi/9)cos(2pi/9)-cos(4pi/9)-1]
cot(alpha)=[1/sin(pi/9)]-cot(4pi/9)-[1/sin(4pi/9)]
=[1/sin(pi/9)]-[1+cos(4pi/9)/sin(4pi/9)]=[1/sin(pi/9)]-cot(2pi/9)
=[2sin(7pi/18)-cos(2pi/9)]/sin(2pi/9)
={2sin[(pi/6)+(2pi/9)]-cos(2pi/9)}/sin(2pi/9)
=[cos(2pi/9)+(sqrt3)sin(2pi/9)-cos(2pi/9)]/sin(2pi/9)=sqrt3
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 61.58.103.35
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1544010251.A.7D3.html
※ 編輯: wayne2011 (61.58.103.35), 12/05/2018 20:44:11
→
12/05 20:52,
7年前
, 1F
12/05 20:52, 1F
※ 編輯: wayne2011 (61.58.103.35), 12/05/2018 20:52:32
→
12/05 21:39,
7年前
, 2F
12/05 21:39, 2F
討論串 (同標題文章)