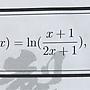[微積] 級數

看板Math作者 (阿中)時間8年前 (2017/11/23 00:20), 8年前編輯推噓3(3推 0噓 6→)
留言9則, 4人參與, 8年前最新討論串1/4 (看更多)
https://i.imgur.com/aPBjYfV.jpg
請問為何積分從1到無限大 可以想成級數呢 我感覺這是不太相同的東西 目前只知道有積分審斂法 可是這題也不是阿 還是說這就是固定做法？ -- ※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 119.77.150.53 ※ 文章網址: https://www.ptt.cc/bbs/Math/M.1511367618.A.09A.html ※ 編輯: aabbcc610 (119.77.150.53), 11/23/2017 00:21:18
→
11/23 00:21, 8年前 , 1F
泰勒展開?
11/23 00:21, 1F
推
11/23 09:42, 8年前 , 2F
只是把sin(x*x)這個東西用級數表示而已啊，兩個相等
11/23 09:42, 2F
推
11/23 12:00, 8年前 , 3F
只是sin的級數展開而已 cos跟e也都有 可以一起背吧
11/23 12:00, 3F
我的問題不是展開那邊喔 我是說為何最後積分一到無限大 可以直接轉換成比值審斂法 ※ 編輯: aabbcc610 (119.77.150.53), 11/23/2017 12:05:25
推
11/23 12:23, 8年前 , 4F
那是alternating series吧
11/23 12:23, 4F
→
11/23 12:26, 8年前 , 5F
不過代無限大收斂的確蠻神奇的
11/23 12:26, 5F
→
11/23 12:26, 8年前 , 6F
姑且代任意R進去都會收斂 但不代表無限大會收斂啊(?
11/23 12:26, 6F
→
11/23 12:28, 8年前 , 7F
我會換成 int_1^inf sin(x)/2sqrt(x) dx
11/23 12:28, 7F
→
11/23 12:28, 8年前 , 8F
照 sin(x)=0 的地方拆成無窮級數
11/23 12:28, 8F
→
11/23 12:29, 8年前 , 9F
然後再用alternating series證明收斂
11/23 12:29, 9F
‣ 更多 aabbcc610 的文章
文章代碼(AID): #1Q5QF22Q (Math)
討論串 (同標題文章)
完整討論串 (本文為第 1 之 4 篇)：
排序： 最新先 | 最舊先 | 留言數
微積
3
7
[微積] 級數 級數
arro04999
5年前, 02/12
微積
2
7
[微積] 級數 級數
ivan2684716
7年前, 06/12
微積
1
2
[微積] 級數 級數
aabbcc610
8年前, 12/02
微積
3
9
[微積] 級數 級數
aabbcc610
8年前, 11/23
在新視窗開啟完整討論串 (共4篇)
‣ 更多 aabbcc610 的文章
文章代碼(AID): #1Q5QF22Q (Math)