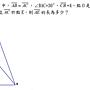
Re: [中學] 國三外心問題

看板Math作者wayne2011 (今年十三號星期五)時間8年前 (2017/11/22 11:32)推噓0(0推 0噓 0→)

留言0則, 0人參與討論串3/3 (看更多)

※ 引述《swearit (事事豈能盡如人意)》之銘言： : https://i.imgur.com/KhlFcua.png

: 如題,用正弦定理此題即可迅速求出,想請教如果以國三學生的程度求解,有甚麼方式, : 感謝各位從E點至OC,OA兩邊畫高使之垂足為F,G 即可知道 "兩高比"即為"底邊比" 亦即 CE/EA=EF/GE=4cos(pi/6)/{2[(sqrt6)+(sqrt2)]*cos(5pi/12)]}=sqrt3 可設EF=(sqrt3)k,GE=k 則C點至OA高=k(sqrt3+1)=[2(sqrt6+sqrt2)]*cos(5pi/12)=2...viviani定理 k=(sqrt3)-1,[3-(sqrt3)]=CE*sin(pi/12)=(2sqrt6),EA=2sqrt2. -- ※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 61.58.103.35 ※ 文章網址: https://www.ptt.cc/bbs/Math/M.1511321557.A.0BE.html ※ 編輯: wayne2011 (61.58.103.35), 11/25/2017 10:49:52 ※ 編輯: wayne2011 (61.58.103.35), 11/25/2017 10:50:15

‣ 返回看板[ Math ] 數學

‣ 更多 wayne2011 的文章

文章代碼(AID): #1Q5E_L2- (Math)