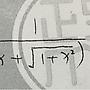Re: [微積] 政大碩士考古題

: 求解
: 感謝各位大大
原式
ln(1 + x) - ln(x + √[1 + x^2])
= lim ----------------------------------
x->0 ln[x + √[1 + x^2]] ln[1 + x]
ln(1 + x) - arcsinh(x)
= lim -----------------------------
x->0 arcsinh(x) ln(1 + x)
1/(1 + x) - 1/√[x^2 + 1]
= lim -----------------------------------------------
x->0 [ln(1 + x)]/√[x^2 + 1] + arcsinh(x)/(1 + x)
√[x^2 + 1] - (1 + x)
= lim ------------------------------------------------
x->0 [ln(1 + x)](1 + x) + √[x^2 + 1] * arcsinh(x)
(x/√[x^2 + 1]) - 1
= lim -----------------------------------------------
x->0 1 + ln(1 + x) + xarcsinh(x)/√[x^2 + 1] + 1
-1
= --------------
2
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 111.249.188.248
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1485886120.A.D0B.html
推
02/01 11:55, , 1F
02/01 11:55, 1F
→
02/01 22:51, , 2F
02/01 22:51, 2F
→
02/01 22:52, , 3F
02/01 22:52, 3F
→
02/03 00:24, , 4F
02/03 00:24, 4F
討論串 (同標題文章)