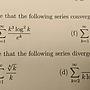Re: [分析] 高微4題

看板Math作者Eliphalet (系統過宅)時間10年前 (2015/12/23 18:11)推噓2(2推 0噓 1→)

留言3則, 3人參與討論串2/2 (看更多)

※ 引述《tong70624 (小曹)》之銘言： : 麻煩各位大大幫忙解答了~ : 最近開始不知道高微在講什麼了QQ : http://i.imgur.com/yU1joGL.jpg

上面的 (d) 對足夠大的正整數 k ， e^k > k^7 又已知 log k < k ，因此會收斂上面的 (f) 已知 log(.) 遞增到正無窮，因此對足夠大的 k 1/k^(log(k)) < 1/k^2，因此會收斂下面的 (b) 已知 k^(1/k) 皆大於 1，因此 k^(1/k)/k > 1/k，因此會發散下面的 (d) p 小於等於 0 顯然發散；又當 p 大於 0 小於 1 時以及 p = 1 時，皆可由積分測試法得發散的結果大致這樣吧... -- ※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 114.46.224.228 ※ 文章網址: https://www.ptt.cc/bbs/Math/M.1450865471.A.984.html

推

tong70624

12/23 18:34, , 1^F

12/23 18:34, 1^F

→

kevinmath

12/23 19:04, , 2^F

12/23 19:04, 2^F

為了方便湊 1/k^2 而已... 而且事實上不用到 7，大於 4 就好了 ※ 編輯: Eliphalet (114.46.224.228), 12/23/2015 19:31:30

推

Pieteacher

12/23 19:36, , 3^F