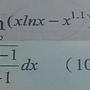Re: [微積] 一題lim趨近 一題積分

: 第一題我一開始覺得是羅必達法則 無限大-無限大的
: 但似乎分式可通分的才能用羅必達,這題可能要用夾擠法
: 請板友們提點一下。
為什麼,為什麼,又出現這題...
我至少回過兩次這題 XD
是高考的出題者很熱愛這題目嗎
原式 = x * ( ln(x) - x^(0.1))
ln(x) ln(x) 10 ln(x^0.1)
已知 lim --------- = 0 , 故 ------------ = --------------- →0
x→∞ x x^(0.1) x^(0.1)
當 x→∞。
所以原極限為 -∞
: 第二題感覺是很簡單的積分,但我用令u=(x-1)^0.5的積分的結果我不會算
: 也麻煩版友了!
: 謝謝大家
u=(x-1)^0.5 可以算啊 , 這樣可以把該積分變成
1 2u^2 1 du
∫ ---------- du = 2 - 4 ∫ -------
0 u^2 + 2 0 u^2+2
= 2 - 2√2 * atan(√2/2)
如果我沒算錯的話,這應該是題目數字配得不好
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 114.46.213.101
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1431524409.A.B0C.html
→
05/14 00:04, , 1F
05/14 00:04, 1F
推
05/14 17:44, , 2F
05/14 17:44, 2F
討論串 (同標題文章)
本文引述了以下文章的的內容:
完整討論串 (本文為第 2 之 2 篇):