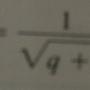Re: [微積] 求救一題找導函數

看板Math作者LuisSantos (但願真的能夠實現願望)時間11年前 (2014/07/11 23:02)推噓1(1推 0噓 0→)

留言1則, 1人參與討論串2/2 (看更多)

※ 引述《jouen (呵呵)》之銘言： : http://i.imgur.com/2g3dbvV.jpg

: 下圖是我卡住的地方 : X-q不知道什麼方法消掉 : 還是有其它比較好的算法呢？ : 求解 √(q+1) - √(x+1) lim ---------------------------- x→q (x - q)(√(x+1))(√(q+1)) (√(q+1) - √(x+1))(√(q+1) + √(x+1)) = lim -------------------------------------------- x→q (x-q)(√(x+1))(√(q+1))(√(q+1) + √(x+1)) (q+1) - (x+1) = lim ------------------------------------------ x→q (x-q)(√(x+1))(√(q+1))(√(q+1) + √(x+1)) q - x = lim ------------------------------------------- x→q (x-q)(√(x+1))(√(q+1))(√(q+1) + √(x+1)) -(x-q) = lim ------------------------------------------- x→q (x-q)(√(x+1))(√(q+1))(√(q+1) + √(x+1)) -1 = lim --------------------------------------- x→q (√(x+1))(√(q+1))(√(q+1) + √(x+1)) -1 = --------------------------------------- (√(q+1))(√(q+1))(√(q+1) + √(q+1)) -1 -1 -3 = ------------------- = (---)((q+1)^(---)) (q+1)(2)(√(q+1)) 2 2 -- ※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 114.36.163.166 ※ 文章網址: http://www.ptt.cc/bbs/Math/M.1405090944.A.5BB.html

推

jouen

07/11 23:33, , 1^F

07/11 23:33, 1^F

‣ 返回看板[ Math ] 數學

‣ 更多 LuisSantos 的文章

文章代碼(AID): #1Jl_o0Mx (Math)