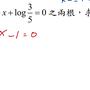Re: [中學] 指對數
※ 引述《adamchi (adamchi)》之銘言:
: 方程式 (logx)^2-[logx]-2 = 0
: 其中[logx]表示logx的高斯符號
: 試求方程式的解(有三個解)
方程式可以改寫成 (logx)^2 = [logx]+2
當 logx > 2 時, (logx)^2 > 2logx = logx + logx > [logx] + 2
所以 logx <= 2
但 [logx] = (logx)^2 -2 >= -2
所以我們只要分別就 [logx] = -2, -1, 0, 1, 2 去討論就好了
--
※ 發信站: 批踢踢實業坊(ptt.cc)
◆ From: 220.132.177.99
討論串 (同標題文章)