Re: [閒聊] 每日LeetCode已回收

看板Marginalman作者Rushia (みけねこ的鼻屎)時間2年前 (2023/01/11 11:18)推噓2(2推 0噓 1→)

留言3則, 3人參與討論串188/719 (看更多)

1443. Minimum Time to Collect All Apples in a Tree 給你一個n表示節點數量、一個edges[]表示樹之間的關係，和一個hasApple[i]表示 node i 是否有蘋果，我們要從節點0出發(root)並且拿到所有蘋果後走回原點，求出共要走幾步(取最少)。 Example： https://assets.leetcode.com/uploads/2020/04/23/min_time_collect_apple_1.png

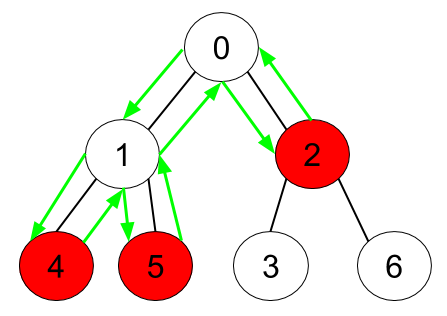
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,true,true,false] Output: 8 https://assets.leetcode.com/uploads/2020/04/23/min_time_collect_apple_2.png

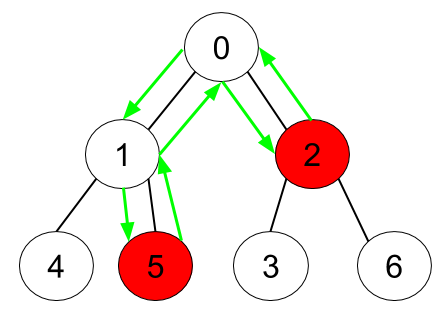
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,false,true,false] Output: 6 Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,false,false,false,false,false] Output: 0 思路： 1.用list建立邊的關係，並統計蘋果的數量，如果蘋果數量為0直接返回0。 2.大致上的想法是拿所有必要的成本，拜訪每個點的成本為2(來回) 有兩種情況當前節點的成本必拿： (1)子節點有蘋果 (2)當前點有蘋果其他情況的成本都捨棄 3.用dfs取出所有必要的節點之後減去2(走到節點0不需要成本) Java Code： ----------------------------------------- class Solution { private List<List<Integer>> graph; private List<Boolean> hasApple; public int minTime(int n, int[][] edges, List<Boolean> hasApple) { graph = new ArrayList<>(); this.hasApple = hasApple; int apples = 0; for (int i = 0; i < n; i++) { graph.add(new ArrayList<>()); if (hasApple.get(i)) { apples++; } } if (apples < 1) { return 0; } for (int[] edge : edges) { graph.get(edge[0]).add(edge[1]); graph.get(edge[1]).add(edge[0]); } return dfs(0, -1) - 2; } private int dfs(int start, int prev) { int cost = 0; for (int edge : graph.get(start)) { if (edge == prev) continue; cost += dfs(edge, start); } if (cost > 0 || hasApple.get(start)) { cost += 2; } return cost; } } ----------------------------------------- -- https://i.imgur.com/sjdGOE3.jpg