看板
[ Math ]
討論串[中學] 一題直線與圓
共 6 篇文章
內容預覽:
設直線PQ:y-2=m(x-1). y=m(x-1)+2,代入x^2+y^2=37. x^2+[m(x-1)+2]^2=37 ,(m^2+1)x^2+2m(2-m)x+(m^2-4m-33)=0. 令P(x1,y1),Q(x2,y2). x1+x2=2m(m-2)/(m^2+1),x1x2=[(m-
(還有200個字)
內容預覽:
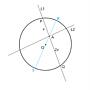
這題用幾何解比較不需要什麼複雜計算. 首先要先確認 符合這題條件的弦一般情況下會有兩條 的事實. 那我們就可以來隨便畫個圖,做點假設順便把過A直徑RS畫出來. https://i.imgur.com/BozhJjJ.png. 既然OA=√5. →RA=√37-√5, AS=√37+√5. PA*AQ
(還有385個字)
內容預覽:
(1) 參考. 陳一理. 所編著的"錐線". 設P(2cost,2sint)為圓與直線切點. 則過P切線為(2cost)x+(2sint)y=4. (cost)x+(sint)y=2. 與(x/a)+(y/b)=1比較係數後. cost/(2/a)=sint/(2/b)=1,消去參數後,(a^2)(
(還有30個字)