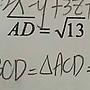看板 [ Math ]
討論串[中學] 一題體積問題請教~
共 4 篇文章
內容預覽： 開啟 | 關閉 | 只限未讀
首頁
上一頁
1
下一頁
尾頁
#4
Re: [中學] 一題體積問題請教~
推噓0(0推 0噓 0→)留言0則，0人參與, 最新作者wayne2011 (泡麵夜清明兒童節)時間7年前 (2018/04/04 11:11), 編輯資訊
0
1
0
內容預覽:
參考. 凡異出版的"立幾34講". 當中ch2的ex5. AB=CD=sqrt29,DA=BC=sqrt13,CA=BD=sqrt34. V=(1/12)sqrt[2(c^2+a^2-b^2)(a^2+b^2-c^2)(b^2+c^2-a^2)]. =(1/12)sqrt[2(34+29-13)(2
(還有23個字)
#3
Re: [中學] 一題體積問題請教~
推噓0(0推 0噓 0→)留言0則，0人參與, 最新作者tzhau (生命中無法承受之輕)時間7年前 (2018/04/03 00:38), 7年前編輯資訊
0
1
0
內容預覽:
AB = CD = sqrt(5^2 + 2^2). AC = BD = sqrt(5^2 + 3^2). AD = BC = sqrt(2^2 + 3^2). 作一個長寬高分別為5,3,2的長方體. 則所求四面體的體積即為長方體體積扣掉四個角落所剩下的部分. 故所求 = 5x3x2-4x(1/6)
(還有31個字)
#2
Re: [中學] 一題體積問題請教~
推噓2(2推 0噓 10→)留言12則，0人參與, 7年前最新作者chemmachine (chemmachine)時間7年前 (2018/04/02 19:29), 編輯資訊
0
1
1
內容預覽:
已知四面體六邊長，欲求四面體體積，we have the following result：. https://imgur.com/a/JKn72. --. ※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 218.161.61.7. ※ 文章網址: https://www.ptt.cc/bbs
#1
[中學] 一題體積問題請教~
推噓1(1推 0噓 1→)留言2則，0人參與, 7年前最新作者nokol (騷人墨客)時間7年前 (2018/04/02 17:55), 編輯資訊
0
1
0
內容預覽:
http://i.imgur.com/4HFzoGo.jpg. 想請教站上大師指點. 謝謝你，謝謝。. -----. Sent from JPTT on my Samsung SM-G955F.. --. ※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 101.10.37.101. ※ 文章網
首頁
上一頁
1
下一頁
尾頁