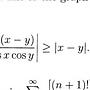Re: [微積] 一題證明

: 請問第三題該怎麼證明呢?
如果不是常數函數,那一定有兩點函數值不同。
再根據 MVT,一定有一個 f'≠0 的地方。
正的那邊寫起來跟負的沒差多少,假設 f'(a)<0 for some a。
因為 f' 遞增,所以在 a 左邊的 x,f'(x)≦f'(a)。
所以 f(x)=f(a)-∫_x^a f'(t)dt≧f(a)-f'(a)*(a-x),
上面這行用微分寫的話就是
[ f(x)-f(a) ]/(x-a)=f'(c)≦f'(a),因為 x<c<a。
而只要找負很大的 x,RHS 就可以任意地大,即 f(x) 一定可以超過 1,矛盾。
微分版本繼續寫的話就是
讓 x→-∞,LHS→0,所以 0≦f'(a),矛盾。
重點就是 f≧任何一條切線的函數形式,
如果 f 不是常數,那就會大於等於一個一次函數,很容易就超過 1 了。
有些 f 只遞減不遞增,例如 exp(-x),
當然也有只遞增不遞減的 f。
所以 f'(a) 的正負必須提出來討論。
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 61.230.130.38
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1549805169.A.E93.html
推
02/10 22:17,
6年前
, 1F
02/10 22:17, 1F
推
02/10 22:19,
6年前
, 2F
02/10 22:19, 2F
→
02/10 23:10,
6年前
, 3F
02/10 23:10, 3F
→
02/10 23:25,
6年前
, 4F
02/10 23:25, 4F
推
02/10 23:54,
6年前
, 5F
02/10 23:54, 5F
※ 編輯: Vulpix (61.230.130.38), 02/11/2019 22:25:28
討論串 (同標題文章)