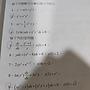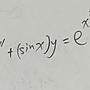Re: [微積] ODE
※ 引述《oblivion87 (oblivion87)》之銘言:
: 毫無頭緒,只想出這個幾乎是亂猜的方法,請問這樣判斷可以嗎,還是要硬級數解呢,有
: 什麼比較嚴謹的證明方法嗎?
: https://i.imgur.com/3Cyv9f7.jpg

你的題目應該是:
f"+f=0, (x+1)g"+xg=0 for x>0, both f and g are not trivial,
show that there is a zero of f between any consecutive zeroes of g.
pf):
Take two consecutive zeroes of g, say a and b, where a < b.
suppose that there is no zero of f in (a,b),
then f remains its sign on (a,b), say positive.
WLOG, we may assume that g is positive on (a,b) as well.
f"g-fg" = -fg+fgx/(x+1) = -fg/(x+1)
Integrate the previous equation on (a,b), we get
f'(b)g(b)-f(b)g'(b)-f'(a)g(a)+f(a)g'(a) = -∫_a^b fg/(x+1) dx
=> -f(b)g'(b)+f(a)g'(a) = -∫_a^b fg/(x+1) dx
, where RHS < 0.
By definition, g'(a)≧0 and g'(b)≦0.
They cannot be 0, since g'(a) = 0 implies g = 0.
So g'(a) > 0 and g'(b) < 0, hence LHS≧0, a contradiction.
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 163.13.112.58
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1545025905.A.6AE.html
推
12/17 21:12,
7年前
, 1F
12/17 21:12, 1F
→
12/17 21:12,
7年前
, 2F
12/17 21:12, 2F
→
12/17 21:13,
7年前
, 3F
12/17 21:13, 3F
→
12/17 21:14,
7年前
, 4F
12/17 21:14, 4F
→
12/17 21:15,
7年前
, 5F
12/17 21:15, 5F
推
12/17 21:40,
7年前
, 6F
12/17 21:40, 6F

→
12/17 21:53,
7年前
, 7F
12/17 21:53, 7F
※ 編輯: Vulpix (61.230.70.207), 12/29/2018 12:13:13
討論串 (同標題文章)