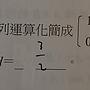Re: [中學] 矩陣
※ 引述《cheesesteak (牛排‧起司)》之銘言:
: 設A, X, Y均為二階方陣
: 其中A之a11=1, a12=4, a21=3, a22=2
: 且X+Y=I, XY=零矩陣, aX+bY=A
: a, b為常數且a>b, 試求a, b之值
A = aX + bY = (a-b)X + b(X+Y)
=> AY = bY
由 XY = 0 , 如果 detY 不等於 0 , 則 X = 0
因此 Y = I (這不合)
所以 Y 為不可逆矩陣,可知列向量成比例,
亦即 Y = [y_11, ky_11; y_21, ky_22]
而且 [y_11,y_21]^T 不為 0 向量
由 AY = bY , 可得 det(A-bI) = 0 故 b = -2 或 5
同理, A^T X^T = a X^T 可得 det(A^T-aI) = 0 故 a = -2 或 5
又 a > b 故 a = 5 , b = -2
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 114.46.223.126
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1432532097.A.E38.html
→
05/25 14:34, , 1F
05/25 14:34, 1F
→
05/25 14:45, , 2F
05/25 14:45, 2F
推
05/25 15:02, , 3F
05/25 15:02, 3F
討論串 (同標題文章)