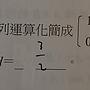[中學] 矩陣

看板Math作者 (書呆)時間11年前 (2014/06/27 11:50), 編輯推噓4(4推 0噓 25→)
留言29則, 4人參與, 6年前最新討論串3/22 (看更多)
題目我用 word 打好了 用成圖片上傳 http://imgur.com/zpGXpY9
主要想要問的是(4) b-c 的最小值是多少 我也只能得到最下面的資訊而已 第(4)個答案沒有，所以也不知道確切的值 麻煩大家了 -- ※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 220.143.71.158 ※ 文章網址: http://www.ptt.cc/bbs/Math/M.1403841013.A.C00.html
→
06/27 15:56, , 1F
把他乘一乘 加一加...
06/27 15:56, 1F
→
06/27 15:57, , 2F
a^2+bc+2a+5 = 0 ... (1)
06/27 15:57, 2F
→
06/27 15:57, , 3F
ab+bd+2b = 0 ... (2)
06/27 15:57, 3F
→
06/27 15:57, , 4F
ac+cd+2c = 0 ... (3)
06/27 15:57, 4F
→
06/27 15:57, , 5F
bc+d^2+2d+5 = 0 ... (4)
06/27 15:57, 5F
→
06/27 15:59, , 6F
(1) - (4) : (a-d)(a+d+2)=0
06/27 15:59, 6F
→
06/27 15:59, , 7F
BY (2) : b(a+d+2)=0
06/27 15:59, 7F
→
06/27 15:59, , 8F
BY (3) : c(a+d+2)=0
06/27 15:59, 8F
→
06/27 16:00, , 9F
所以只要a+d+2 = 0，b c應該可以是任意數?
06/27 16:00, 9F
→
06/27 16:00, , 10F
等等，結論好像不太對，我想想
06/27 16:00, 10F
→
06/27 16:08, , 11F
不過，如果a+d+2不等於0時，可以肯定a=d b=c=0
06/27 16:08, 11F
→
06/27 16:08, , 12F
這時的b-c = 0，所以|b-c| = 0
06/27 16:08, 12F
→
06/27 16:09, , 13F
但這樣的a d無實數解
06/27 16:09, 13F
→
06/27 16:17, , 14F
所以確定 a+d+2=0，剩下(1) (4)可用
06/27 16:17, 14F
推
06/27 16:33, , 15F
把a+d=-2,(1),(4)綜合在一起就是原PO圖片最後兩行吧?
06/27 16:33, 15F
→
06/27 16:39, , 16F
我的意思是，這樣b-c好像沒辦法確定
06/27 16:39, 16F
→
06/27 16:40, , 17F
也找不到方法限制範圍
06/27 16:40, 17F
→
06/27 16:40, , 18F
可能還是可以知道 bc 的範圍吧
06/27 16:40, 18F
→
06/27 16:43, , 19F
但對|b-c|好像沒幫助，或著說我目前還沒找到
06/27 16:43, 19F
→
06/27 16:46, , 20F
或許可以參考 |b+(-c)| >= 2√(-bc) , 若 bc<0
06/27 16:46, 20F
推
06/27 20:53, , 21F
a+d=-2 可推得 ad <= 1, 所以 bc = ad-5 <= -4
06/27 20:53, 21F
→
06/27 20:53, , 22F
再套我樓上應該就可得到極值是 4
06/27 20:53, 22F
→
06/27 20:55, , 23F
呃上一行不太對 QQ
06/27 20:55, 23F
→
06/27 20:56, , 24F
咦好像沒問題...因為 -bc >= 4 不等式串起來了
06/27 20:56, 24F
→
06/27 20:56, , 25F
這樣 |b+(-c)| >= 2√(-bc) >= 2√4 = 4 應該是對的
06/27 20:56, 25F
推
06/27 20:59, , 26F
問題是，ad有可能同為負啊？
06/27 20:59, 26F
→
06/27 21:02, , 27F
沒事我懂了，就算同為負最大也只會是1
06/27 21:02, 27F
推
06/28 02:10, , 28F
ad<=1 是這樣推來的: ad=a(-2-a)=-a^2-2a=-(a+1)^2+1
06/28 02:10, 28F
→
07/07 12:19, 6年前 , 29F
07/07 12:19, 29F
‣ 更多 booksy 的文章
文章代碼(AID): #1JhEdrm0 (Math)
討論串 (同標題文章)
完整討論串 (本文為第 3 之 22 篇)：
排序： 最新先 | 最舊先 | 留言數
中學
6
13
[中學] 矩陣 矩陣
riemannchen
5年前, 05/01
中學
1
3
[中學] 矩陣 矩陣
susiseptem
5年前, 03/22
中學
1
1
[中學] 矩陣 矩陣
ttPttPtt
6年前, 06/18
中學
0
5
[中學] 矩陣 矩陣
irpolo1
6年前, 05/31
中學
1
1
Re: [中學] 矩陣 Re: 矩陣
Poincare
6年前, 05/10
中學
0
1
[中學] 矩陣 矩陣
irpolo1
6年前, 05/10
中學
2
5
[中學] 矩陣 矩陣
irpolo1
6年前, 05/09
中學
3
4
[中學] 矩陣 矩陣
harryeton1
8年前, 05/01
中學
0
4
[中學] 矩陣 矩陣
rita42027
9年前, 05/11
在新視窗開啟完整討論串 (共22篇)
‣ 更多 booksy 的文章
文章代碼(AID): #1JhEdrm0 (Math)