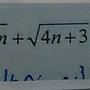[微積] 極限
(n+3)^(1/2) -(n-2)^(1/2)
Lim __________________________ = ?
n→∞ (2n+1)^(1/2)-(2n-3)^(1/2)
(A)0 (B)5*2^(1/2)/4 (C)5/2 (D)不存在
ANS (B)
這題是我弟高職的模擬考題
我解了很久
有沒有更好的做法
(n+3)^(1/2) -(n-2)^(1/2)
Lim __________________________
n→∞ (2n+1)^(1/2)-(2n-3)^(1/2)
1 (2n+6)^(1/2)-(2n-4)^(1/2)
=________ Lim __________________________
2^(1/2) n→∞ (2n+1)^(1/2)-(2n-3)^(1/2)
1 (2+6/n)^(1/2)-(2-4/n)^(1/2)
=________ Lim ___________________________
2^(1/2) n→∞ (2+1/n)^(1/2)-(2-3/n)^(1/2)
1 (2+6t)^(1/2)-(2-4t)^(1/2)
=________ Lim ___________________________
2^(1/2) t→0 (2+t )^(1/2)-(2-3t)^(1/2)
1 [ (2+6t)^(1/2)-(2-4t)^(1/2) ]/t
=________ Lim _________________________________
2^(1/2) t→0 [ (2+t )^(1/2)-(2-3t)^(1/2) ]/t
1 Lim [ (2+6t)^(1/2)-(2-4t)^(1/2) ]/t
=________ _____________________________________
2^(1/2) Lim [ (2+t )^(1/2)-(2-3t)^(1/2) ]/t
1 10f'(2)
=________ _______ ,f(x)= x^(1/2)
2^(1/2) 4 f'(2)
1 5
=________ __
2^(1/2) 2
5*2^(1/2)
=___________
4
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 122.121.24.149
※ 文章網址: http://www.ptt.cc/bbs/Math/M.1396495562.A.260.html
推
04/03 11:43, , 1F
04/03 11:43, 1F
討論串 (同標題文章)