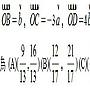Re: [中學] 向量
※ 引述《jimmychad (吉米)》之銘言:
: 設G為三角型OAB重心,P與 Q分別在OA與OB上,
: 且G,P,Q三點共線,若OP=3/4OA,OQ=nOB,則n=?
: 我只想到GA+GB+GO=0
: OA-OG+OB-OG+GO=0
: 3OG+OA+OB=0
^^^少一個負號
: 接下來不知道怎麼辦了
: 請各位高手解答
賺個P幣
OG=(1/3)OA+(1/3)OB (由你推得的那個條件)
=(4/9)OP+(1/3n)OQ (由題目給的條件)
由P,G,Q三點共線 => (4/9)+(1/3n)=1 => n=3/5
此類問題換成內心、垂心、外心都可以用這個過程
將OG換成OA,OB的線性組合,再利用題目條件換成OP,OQ組合
最後利用三點共線,線性組合之係數和為1,解得所求!
--
※ 發信站: 批踢踢實業坊(ptt.cc)
◆ From: 123.241.32.132
討論串 (同標題文章)