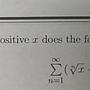[微積] 極限

看板Math作者 (nono)時間12年前 (2013/11/02 22:57), 編輯推噓5(5推 0噓 20→)
留言25則, 8人參與, 6年前最新討論串27/61 (看更多)
求 00 1 Σ ─(-1)^(n+1) n=1 n 我知道答案是 ln2 可是我如果把級數展開 1 1 1 => lim (1-─+─-─....) n->00 2 3 4 1 1 1 1 1 1 = lim (1+─+─+─....) -2*lim(─+─+─+...) n->00 2 3 4 2 4 6 1 1 1 1 1 1 1 = lim (1+─+─+─....) -2*(─)lim (─+─+─+...) n->00 2 3 4 2 n->00 1 2 3 = 0 ??? 請問我哪裡做錯了??? -- ※ 發信站: 批踢踢實業坊(ptt.cc) ◆ From: 111.253.32.18
推
11/02 23:00, , 1F
請問第一個等式怎來的呢
11/02 23:00, 1F
→
11/02 23:01, , 2F
lim (f+g) = lim f +lim g 是有條件的
11/02 23:01, 2F
推
11/02 23:02, , 3F
因為這個數列是conditional convergence 不是
11/02 23:02, 3F
→
11/02 23:02, , 4F
absolute convergence 所以改變順序之後相加 值不同
11/02 23:02, 4F
x 1 ln|1+x| = ∫── dt 0 1+t 再利用 1 1 ── = ──── = 1+(-t)+(-t)^2+..... , -1<t<1 1+t 1-(-t) ※ 編輯: nobrother 來自: 111.253.32.18 (11/02 23:07)
→
11/02 23:03, , 5F
交錯級數收斂的話 有些重排會改變級數和
11/02 23:03, 5F
→
11/02 23:04, , 6F
條件收斂重排會改變級數和 沒記錯的話這題試試看
11/02 23:04, 6F
→
11/02 23:04, , 7F
對ln(1+x)對x=0做泰勒展開
11/02 23:04, 7F
→
11/02 23:11, , 8F
不好意思 我對重排不太了解 那麼樣算是正常的排法?
11/02 23:11, 8F
→
11/02 23:12, , 9F
所以不是絕對收斂就要用積分的式子算嗎
11/02 23:12, 9F
推
11/02 23:13, , 10F
原本你列出來的第一個式子 按照定義是先算 sum n=1
11/02 23:13, 10F
→
11/02 23:14, , 11F
to m, 算出每個m的上面算是的值 稱為s_m 然後再取
11/02 23:14, 11F
→
11/02 23:15, , 12F
lim m-> infinity s_m
11/02 23:15, 12F
→
11/02 23:15, , 13F
你展開之後的第一個級數發散呀~
11/02 23:15, 13F
→
11/02 23:20, , 14F
我知道他發散,但我以為兩個一樣可以相減...
11/02 23:20, 14F
推
11/02 23:21, , 15F
也就是說 sum n=1 to infinity 意思是
11/02 23:21, 15F
→
11/02 23:21, , 16F
lim m -> infinity (sum n=1 to m)
11/02 23:21, 16F
→
11/02 23:22, , 17F
你看一下wiki的conditional convergence, 上面有說
11/02 23:22, 17F
→
11/02 23:22, , 18F
符合一定條件之下的數列 在重新排列之後 總和的極限
11/02 23:22, 18F
→
11/02 23:22, , 19F
可以是任意實數
11/02 23:22, 19F
→
11/02 23:23, , 20F
也就是說你沒做錯什麼 只是要把定義搞清楚 那個總和
11/02 23:23, 20F
→
11/02 23:24, , 21F
的概念不只是對某個集合裡面的數字作加總 還包含了特
11/02 23:24, 21F
→
11/02 23:24, , 22F
定順序。 (如果項數是有限，則順序跟總和無關)
11/02 23:24, 22F
推
11/02 23:58, , 23F
Riemann series thm.
11/02 23:58, 23F
→
01/02 15:35, 7年前 , 24F
也就是說 sum n= https://muxiv.com
01/02 15:35, 24F
→
07/07 11:36, 6年前 , 25F
請問第一個等式怎來的呢 https://noxiv.com
07/07 11:36, 25F
‣ 更多 nobrother 的文章
文章代碼(AID): #1ITHBit6 (Math)
討論串 (同標題文章)
完整討論串 (本文為第 27 之 61 篇)：
排序： 最新先 | 最舊先 | 留言數
微積
0
4
[微積] 極限 極限
ChenYM
1年前, 11/22
微積
2
9
[微積] 極限 極限
ChenYM
1年前, 09/15
微積
5
10
[微積] 極限 極限
lllll12b56
4年前, 05/18
微積
[微積] 極限 極限
xy210742
5年前, 04/21
微積
5
7
[微積] 極限 極限
yuyujack
7年前, 01/07
微積
1
3
[微積] 極限 極限
oblivion87
7年前, 01/03
微積
1
13
[微積] 極限 極限
ivan2684716
7年前, 06/19
在新視窗開啟完整討論串 (共61篇)
‣ 更多 nobrother 的文章
文章代碼(AID): #1ITHBit6 (Math)