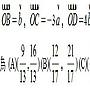[中學] 向量
G點為三角形重心,現於AB、BC、CA上取三點D、E、F
使AD=DB BE=3EC CF=2FA,求當DG=aDE+yDF(向量)時之x、y?
以下英文字母均表向量:
我的想法是
DG=x(1/4 DB + 3/4 DC) + y( 2/3 DA +1/3 DC) ...內分點
=2y/3 DA + x/4 DB + (3x/4 +y/3) DC ...(*)
又因為G為三角形ABC重心
故 OG =1/3 OA +1/3 OB +1/3 OC
令 O=D
DG =1/3 DA +1/3 DB +1/3 DC
和(*)比較係數 => x=4/3 y=1/2 但是為什麼帶入驗算DC答案不會是1/3呢?
請問版上前輩這樣的解法哪裡不對?
謝謝!
又想要問,
如果知道D、E、F三個不共線定點,
也知道如上之AD=DB BE=3EC CF=2FA之類的比例關係,
A、B、C三點可以唯一確定嗎?
(也就是如果知道D、E、F三點坐標,怎麼利用向量反求A、B、C三點最快呢?)
非常謝謝!
--
※ 發信站: 批踢踢實業坊(ptt.cc)
◆ From: 114.36.127.134
推
05/27 12:11, , 1F
05/27 12:11, 1F
→
05/27 12:18, , 2F
05/27 12:18, 2F
討論串 (同標題文章)