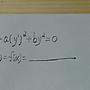[微積] 微分方程

看板Math作者 (Tidus)時間14年前 (2011/11/13 01:48), 編輯推噓2(2推 0噓 9→)
留言11則, 2人參與, 最新討論串14/66 (看更多)
[e^(x+y)+ye^y]dx+[xe^y-1]dy=0 這個非齊次的方程式要怎麼把它搞成齊次的?? 好像不能用找a(x,y)這方法。 -- ※ 發信站: 批踢踢實業坊(ptt.cc) ◆ From: 114.38.164.204
推
11/13 01:59, , 1F
找積分因子讓他變成exact
11/13 01:59, 1F
→
11/13 02:00, , 2F
用I(y)=exp{[(N_x-M_y)/M]dy}
11/13 02:00, 2F
→
11/13 12:45, , 3F
樓上的那個是怎麼找的阿
11/13 12:45, 3F
推
11/13 12:47, , 4F
我課本裡有教學耶 反正想法就是找一個只和x或y有關的
11/13 12:47, 4F
→
11/13 12:47, , 5F
積分因子乘上去讓他變exact
11/13 12:47, 5F
→
11/13 12:48, , 6F
然後推倒的結果 如果[(N_x-M_y)/M] 只跟y有關 或是
11/13 12:48, 6F
→
11/13 12:48, , 7F
[(M_y-N_x)/N]只跟x有關 就可以知道他們的積分因子是
11/13 12:48, 7F
→
11/13 12:49, , 8F
I(y)=e^[int(N_x-M_y)/M dy]
11/13 12:49, 8F
→
11/13 12:50, , 9F
或 I(y)=e^[int (M_y-N_x)/N dx]
11/13 12:50, 9F
→
11/13 12:50, , 10F
應該不少微方課本裡有吧?
11/13 12:50, 10F
→
11/13 14:25, , 11F
我物樹的微分方程沒講到這個說@@
11/13 14:25, 11F
‣ 更多 j0958322080 的文章
文章代碼(AID): #1Elh5nM4 (Math)
討論串 (同標題文章)
以下文章回應了本文：
完整討論串 (本文為第 14 之 66 篇)：
排序： 最新先 | 最舊先 | 留言數
在新視窗開啟完整討論串 (共66篇)
‣ 更多 j0958322080 的文章
文章代碼(AID): #1Elh5nM4 (Math)