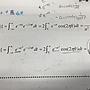Re: [微積] 一題微積分
※ 引述《light0617 (EDWIN)》之銘言:
: 一題微積分
: 題目有點長也蠻難的@@ 沒有詳解
: 懇請板上高手解答~
: A boy,standing in corner A of a rectangular pool,
: has a boat in the adjacent corner B on the end of a 10 meter-long.
: He walks along the side of the pool toward C keeping the string taut.
: Locate the boy and the boat when the latter is 6 meters from AC .
: (hint: choose the coordinate system so that AC is along the x- axis
: and AB is along the y-axis)
: Given:ln3~=1.1
: ans:船的位置(3,6) 男孩的位置(11,0)
: 感恩
畫個醜醜的示意圖
B(0,10) B'為船後來所在位置
|\ A'為小男孩後來所在位置
|\
|﹨
| ‧B'(x,y) 曲線BB'在B'的切線會與A'B'平行
| | \
| |y \ 10 dy y
| | \ 所以--= - ------
| | \ A' dx √(100-y^2)
A ̄ ̄ ̄ ̄ ̄ ̄
x √(100-y^2)
∫√((100/y^2)-1) dy=∫-dx = -x+C
令y=10cosu dy=10d(cosu)
左式=∫10tanu d(cosu)
=10tanu cosu-10∫cosu (secu)^2du
=10sinu-10ln(secu+tanu)= -x+C
x=0, y=10, cosu=1 → C=0
題目問 y=6, 此時cosu=3/5 sinu=4/5
10*(4/5)-10ln(5/3+4/3)=8-10ln3= -x
x≒3 ∴A'(11,0) B'(3,6)
--
※ 發信站: 批踢踢實業坊(ptt.cc)
◆ From: 122.121.208.20
→
07/14 02:54, , 1F
07/14 02:54, 1F
推
07/14 21:37, , 2F
07/14 21:37, 2F
※ 編輯: facebone 來自: 122.121.217.231 (07/15 21:03)
討論串 (同標題文章)