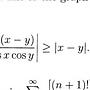Re: [微積] 一題證明
pi x pi pi x
∫x f(sinx) dx = x∫ f(sin t)dt | - ∫ ∫f(sint)dt dx
0 0 0 0 0
pi pi x
= pi*∫ f(sin t)dt - ∫ ∫f(sint) dt dx
0 0 0
pi pi t
= pi*∫ f(sin x)dx - ∫ ∫ f(sint) dx dt
0 0 0
pi pi
= pi*∫ f(sin x)dx - ∫ t f(sin t)dt
0 0
pi pi
=pi*∫ f(sinx)dx - ∫ xf(sinx)dx
0 0
pi pi
=> 2∫xf(sinx)dx = pi∫f(sinx)dx
0 0
pi pi
=> ∫xf(sinx)dx = pi/2 *∫f(sinx)dx
0 0
以上
※ 引述《young11539 (〝☆小小霈★”)》之銘言:
: if f(x) conti. on [0,1]
: then show that
: ∫xf(sinx)dx = (π/2)∫f(sinx)dx
: 積分範圍 [0,π]
: 感激不盡
--
※ 發信站: 批踢踢實業坊(ptt.cc)
◆ From: 114.34.202.142
推
06/05 18:17, , 1F
06/05 18:17, 1F
討論串 (同標題文章)