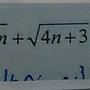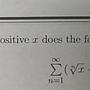[微積] 極限
f(n)= sqrt(1x2)+sqrt(2x3)+...+sqrt[n(n+1)]
n
= sigma sqrt[k(k+1)]
k=1
f(n)
求 lim _____ = ?
n->∞
~ n^2
同學問的作業
感覺很像要用黎曼和來解
像去年台大資工考了一題
1^7+2^7+3^7+...+n^7
lim ___________________
n->∞ n^8
答案是1/8 這用黎曼和可以很簡單的求出
問題是上述題目可以用級數和公式來求,也可以用積分(x^7)來求
但這一題要積sqrt[k(k+1)]也不是
要用級數和也不是...
當然sqrt[k(k+1)]的積分可以用多次的積分技巧來求得
可是高中根本沒教這麼難啊(本人目前高三 這是同學問我的題目)
請問各位大大這題怎麼求&有沒有用高中方法來求出來的方法?
謝謝
--
※ 發信站: 批踢踢實業坊(ptt.cc)
◆ From: 111.243.0.97
討論串 (同標題文章)