Re: [閒聊] 每日LeetCode
※ 引述《ZooseWu (動物園 公告)》之銘言:
: 935. Knight Dialer
: 西洋棋的騎士只能往前兩步後往左或右走一步
: 有一個撥號板如下圖
: https://assets.leetcode.com/uploads/2020/08/18/phone.jpg
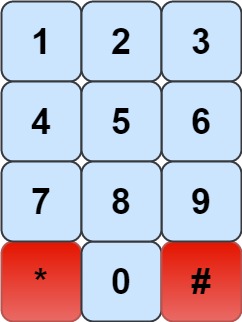
: 騎士只能站在數字上(藍色按鈕)
: 回傳騎士在撥號板上能走的所有可能的數量mod 10^9+7
: Input: n = 1 Output: 10
: 每一格都可以踩 共十種
: Input: n = 2 Output: 20
: 所有可以走的路徑是
: [04, 06, 16, 18, 27, 29, 34, 38, 40, 43,
: 49, 60, 61, 67, 72, 76, 81, 83, 92, 94]
思路差不多 dp[i][j] 代表以數字 i 為結尾 長度是 j 的方法數
像 3 能走到 4, 8
那下一輪的 dp[4][j+1], dp[8][j+1] 就要加上這輪的 dp[3][j]
實際上 j 也不是必要的 因為前面輪數的結果用不到
所以只要記兩輪 也就是這一輪和下一輪的結果就好
Python code:
class Solution:
def knightDialer(self, n: int) -> int:
dp = [1]*10
mod = 10**9+7
edge = [(0,4), (0,6), (1,6), (1,8), (2,7), (2,9), (3,4), (3,8),
(4,9), (6,7)]
for _ in range(n-1):
newdp = [0]*10
for a, b in edge:
newdp[a] += dp[b] % mod
newdp[b] += dp[a] % mod
dp = newdp
return sum(dp) % mod
然後看討論區才發現有個 O(logn) 的做法
因為每一輪的狀態轉移是固定的
可以直接把矩陣列出來 也就是
[[0, 0, 0, 0, 1, 0, 1, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 1, 0, 1, 0],
[0, 0, 0, 0, 0, 0, 0, 1, 0, 1],
[0, 0, 0, 0, 1, 0, 0, 0, 1, 0],
[1, 0, 0, 1, 0, 0, 0, 0, 0, 1],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[1, 1, 0, 0, 0, 0, 0, 1, 0, 0],
[0, 0, 1, 0, 0, 0, 1, 0, 0, 0],
[0, 1, 0, 1, 0, 0, 0, 0, 0, 0],
[0, 0, 1, 0, 1, 0, 0, 0, 0, 0]]
第一行就代表數字 0 下一輪可以變成 4, 6
進行 n 輪就等於是初始狀態 [1,1,1,1,1,1,1,1,1,1]
乘這個矩陣 n-1 次
所以就可以用快速冪 O(logn)
lee真的好強==
--
蛤?
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 118.165.35.201 (臺灣)
※ 文章網址: https://www.ptt.cc/bbs/Marginalman/M.1701062329.A.248.html
→
11/27 13:22,
2年前
, 1F
11/27 13:22, 1F
→
11/27 13:25,
2年前
, 2F
11/27 13:25, 2F
→
11/27 13:27,
2年前
, 3F
11/27 13:27, 3F
→
11/27 13:47,
2年前
, 4F
11/27 13:47, 4F
討論串 (同標題文章)
本文引述了以下文章的的內容:
完整討論串 (本文為第 546 之 719 篇):