Re: [閒聊] 每日LeetCode已回收
1444. Number of Ways of Cutting a Pizza
你有一塊矩形的披薩,上面有一些蘋果,有 k 個小朋友等著吃披薩
你每次都要切下一塊上面有蘋果的披薩交給小朋友,求切法總數 mod 10^9+7
*切法限制水平切或垂直切,水平切交出上半部分,垂直切交出左半部分
Example 1:
https://assets.leetcode.com/uploads/2020/04/23/ways_to_cut_apple_1.png
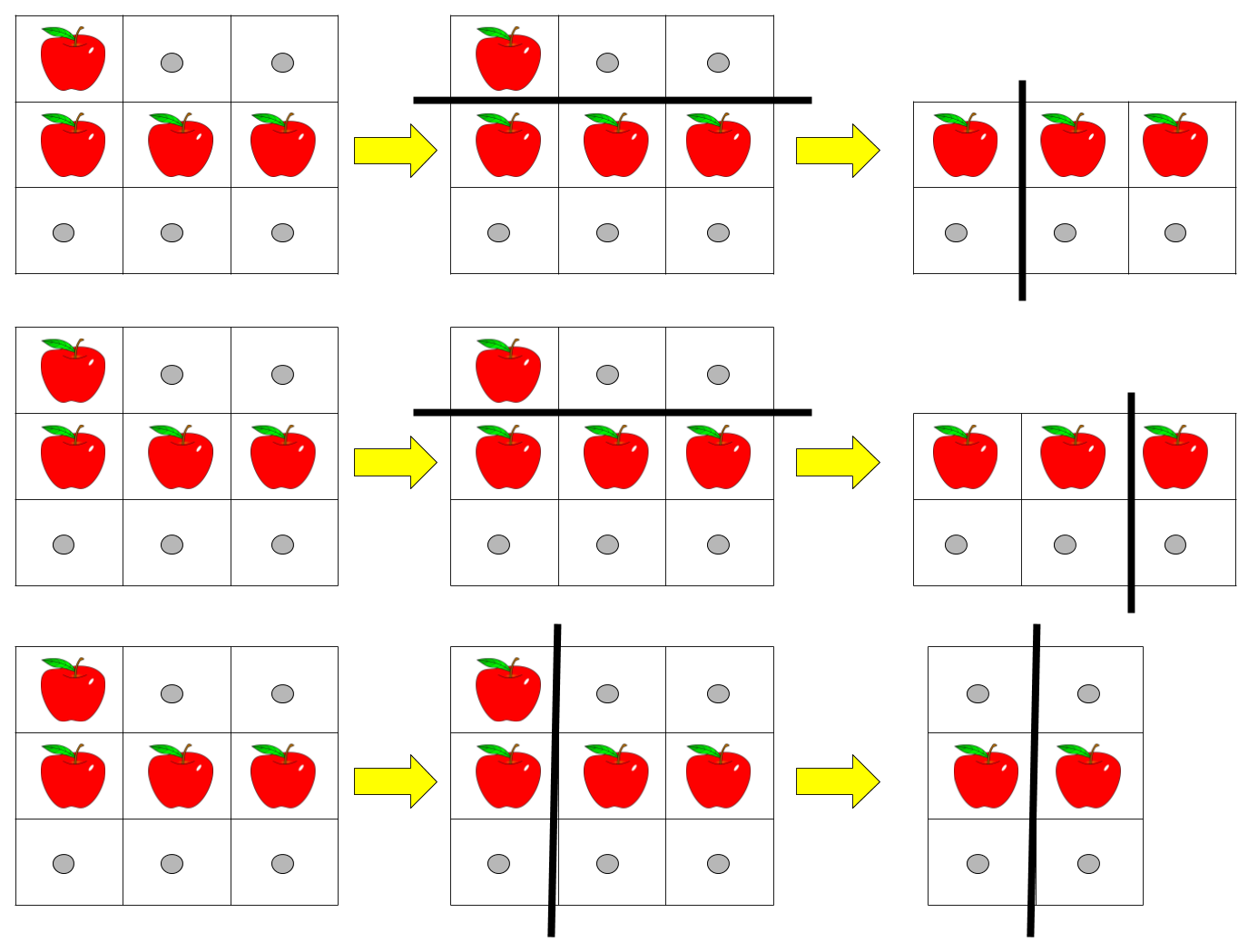
Input: pizza = ["A..","AAA","..."], k = 3
Output: 3
切法如圖
Example 2:
Input: pizza = ["A..","AA.","..."], k = 3
Output: 1
Example 3:
Input: pizza = ["A..","A..","..."], k = 1
Output: 1
思路:
1.切完一刀之後其實就是 k -= 1 後範圍縮小 然後原問題再解一次 馬上想到用dp
假設 dp[0, 0, k] 代表目前的披薩左上角是 (0, 0) 且要分給 k 個小朋友
切法就能寫成 dp[0, 0, k] += dp[i, 0, k-1] for i in range(0~len(pizza)) #水平切
dp[0, 0, k] += dp[0, j, k-1] for j in range(0~len(pizza[0])) #垂直切
像這樣
@cache
def dp(x, y, cut):
if cut == 0:
return 1
res = 0
for i in range(x+1, m):
res += dp(i, y, cut-1)
for i in range(y, n):
res += dp(x, i, cut-1)
return res%mod
2.因為要保證切下的部分必須至少有一塊蘋果 可以用 prefix sum 的概念先建表
apple[i][j] 代表 (i, j) 右下部分的蘋果總數
這樣就能快速算出切這刀有沒有切出蘋果
用上面當例子 水平切就是檢查 apple[0][0] - apple[i][0] 有沒有大於零
垂直切就是檢查 apple[0][0] - apple[0][j]
3.可以順便檢查 apple[i][j] 有沒有比現在的 k 多來剪枝 沒有就直接失敗
Python code:
class Solution:
def ways(self, pizza: List[str], k: int) -> int:
m, n = len(pizza), len(pizza[0])
mod = 10**9+7
apple = [[0]*(n+1) for _ in range(m+1)]
for i in range(m-1, -1, -1):
for j in range(n-1, -1, -1):
apple[i][j] = (pizza[i][j] == 'A') + apple[i][j+1] +
apple[i+1][j] - apple[i+1][j+1]
@cache
def dp(x, y, cut):
if cut == 0:
return 1
res = 0
for i in range(x+1, m):
if apple[x][y] - apple[i][y] > 0 and apple[i][y] >= cut:
res += dp(i, y, cut-1)
for i in range(y, n):
if apple[x][y] - apple[x][i] > 0 and apple[x][i] >= cut:
res += dp(x, i, cut-1)
return res%mod
return dp(0, 0, k-1)
--
蛤?
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 111.251.200.99 (臺灣)
※ 文章網址: https://www.ptt.cc/bbs/Marginalman/M.1680287549.A.E4F.html
→
04/01 02:52,
2年前
, 1F
04/01 02:52, 1F
推
04/01 09:50,
2年前
, 2F
04/01 09:50, 2F
→
04/01 19:42,
2年前
, 3F
04/01 19:42, 3F
討論串 (同標題文章)
完整討論串 (本文為第 277 之 719 篇):