Re: [閒聊] 每日LeetCode已回收

看板Marginalman作者Rushia (みけねこ的鼻屎)時間2年前 (2023/01/26 18:11)推噓1(1推 0噓 1→)

留言2則, 2人參與討論串209/719 (看更多)

787. Cheapest Flights Within K Stops 給你一個邊集合表示的有向圖形，每個邊表示一個航班且都有他的成本，求出從src到 dst的最小成本是多少，你最多只能搭k+1次飛機，若無法到達目的地則返回-1。 Example： https://assets.leetcode.com/uploads/2022/03/18/cheapest-flights-within-k-stops-3drawio.png

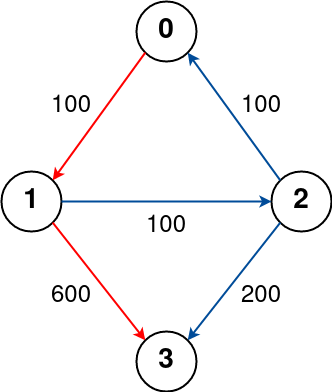
Input: n = 4, flights = [[0,1,100],[1,2,100],[2,0,100],[1,3,600],[2,3,200]], src = 0, dst = 3, k = 1 Output: 700 Explanation: The graph is shown above. The optimal path with at most 1 stop from city 0 to 3 is marked in red and has cost 100 + 600 = 700. Note that the path through cities [0,1,2,3] is cheaper but is invalid because it uses 2 stops. 思路： 1.把航班的邊轉換成一個圖形結構並保存他的成本。 2.從src的位置開始用BFS不斷往外延伸，直到k用完或沒點可以訪問為止。 3.這邊需要做剪枝不然會TLE，若當前點往下一個前往的點的成本比之前算過的成本高的時候，就不把該點加入Queue，下個點就是終點的話也不用繼續訪問。 Java Code： -------------------------------- class Solution { public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) { return BFS(n, flights, src, dst, k); } private int BFS(int n, int[][] flights, int src, int dst, int k) { List<List<int[]>> graph = new ArrayList<>(); for (int i = 0; i < n; i++) { graph.add(new ArrayList<>()); } for (int[] flight : flights) { graph.get(flight[0]).add(new int[] {flight[1], flight[2]}); } int[] ans = new int[n]; Arrays.fill(ans, Integer.MAX_VALUE); Queue<int[]> queue = new LinkedList<>(); queue.offer(new int[] {src, 0}); while (!queue.isEmpty() && k + 1 > 0) { int size = queue.size(); for (int i = 0; i < size; i++) { int[] poll = queue.poll(); for (int[] next : graph.get(poll[0])) { int distance = poll[1] + next[1]; if (distance < ans[next[0]]) { ans[next[0]] = distance; if (next[0] != dst) { queue.offer(new int[] {next[0], distance}); } } } } k--; } return ans[dst] == Integer.MAX_VALUE ? -1 : ans[dst]; } } -------------------------------- -- https://i.imgur.com/bFRiqA3.jpg