Re: [閒聊] 每日LeetCode已回收
2136. Earliest Possible Day of Full Bloom
每朵花有相應的種植時間和成長時間
對第i朵花,需要種plantTime[i]天才能開始成長,一天只能選一朵種
(不一定需要連續,只是總共要花這麼多天種)
需要growTime[i]天生長後開花,花朵可以一起生長
回傳最短能讓所有種子都開花的天數
https://assets.leetcode.com/uploads/2021/12/21/2.png
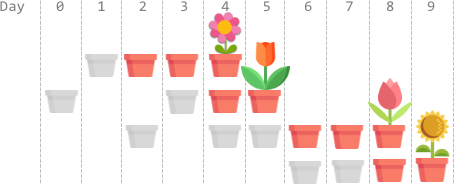
直覺上,因為種是總有一天要種的,
所以會希望要花越多時間生長的要越早完成讓他慢慢長
方法就是,依照growTime排序,之後就越大的越先做
不過重點比較在去證明為什麼這樣會是最佳解:
首先排好序,所以有
growTime_1 >= growTime_2 >= ... >= growTime_n
假設我們的方法需要N天才長完
且是growTime第k大的花在第N天長完
令 M = plantTime_1 + ... + plantTime_k 是第k朵花種完並開始生長的日期
則有 M + growTime_k = N
現在考慮growTime前k大的那些花
他們依舊至少要花M天才能種完全部
也就是,至少其中一朵花要在第M天才種完,假設是第j朵
所以這k朵花開完花的時間就是
M + growTime_j >= M + growTime_k = N (for all j <= k)
(因為growTime_k已經是其中最小的生長時間了)
所以就算光看前k朵花,就不可能有比N還要好的情況
因此N就是最佳解#
去看解答或是一些討論,有些在證明一定要連續種同一朵花到種完為止
不過以單純證明的角度來看的話是不太需要去證這件事
class Solution {
public:
int earliestFullBloom(vector<int>& plantTime, vector<int>& growTime) {
int n = plantTime.size();
vector<int> arg(n);
iota(arg.begin(), arg.end(), 0);
sort(arg.begin(), arg.end(), [&](int i, int j) {
return growTime[i] > growTime[j];
});
int pTime = 0, gTime = 0;
for (int i: arg) {
pTime += plantTime[i];
gTime = max(gTime, pTime + growTime[i]);
}
return gTime;
}
};
好笑的是,如果去看解答的程式碼和我的做比較的話
不能說十分相似,只能說是一模一樣
但實際上這是我在沒看過的情況下一個字一個字打出來的
有點嚇到我= =
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 140.112.16.175 (臺灣)
※ 文章網址: https://www.ptt.cc/bbs/Marginalman/M.1667026587.A.0A7.html
推
10/29 15:04,
3年前
, 1F
10/29 15:04, 1F
推
10/29 18:26,
3年前
, 2F
10/29 18:26, 2F
討論串 (同標題文章)
完整討論串 (本文為第 73 之 719 篇):